*
1. The finite-infinite equivalence principle
According to Pythagorean and Platonic mathematics, everything is simultaneously governed by two principles: The finite and the infinite.1 Composing these coexisting principles into one comprehensive principle, we postulate that everything is governed by the finite-infinite equivalence principle such that everything is both finite and infinite, or, to put it in another way, both one and infinitely many.
If this is true and governs the ultimate reality of everything, then the ultimate and real language of the universe (everything) is not analytic, but instead synthetic, and the numbers that express the complex finite-infinite nature of the universe are not the natural numbers, which are uniquely finite, but the real numbers, which are both finite and infinite. These are some examples of real numbers:
i) The number one: 1 = 0,99999…
ii) The pi number: π = 3.14159…= 3.14
iii) Euler’s number: e = 2.71828… = 3
iv) The Pythagorian number: √2 =1.41421… = 1.4
What they have in common is that each is the limit of an unlimited number of parts. If the limit is denoted by one digit or by a finite number of digits and the unlimited number of parts by an infinite number of digits, we may then conclude that all real numbers are both finite and infinite in agreement with the finite-infinite equivalence principle.
Now, through the compression of the infinite number of digits into one digit or a finite number of digits, our finite neuronal brain and its finite tools “grasp and enclose the infinite, thus bringing infinity to finite beings.”2 Compressing the infinite number of digits into one digit or into a finite number of digits is what we term the finitization process of the infinite undertaken by our finite brain’s faculty of analytic reason (understanding).
The converse process — that is, infinitely expanding the one digit or the finite number of digits, is the infinitization process of the finite undertaken by our infinite mind’s faculties of imagination (intellectual intuition) and infinite synthetic reason. Mathematicians and scientists continuously and unconsciously perform these two processes. It is the way that science progresses in its effort to observe the unobservable and realize the impossible. Based on the above line of synthetic reasoning, let us examine the nature of space and its significance in comprehending the real language of the universe.
The diagonal of the Pythagorean square is the geometric topos of the complex whole
All things are related to one another by the ratio of their numbers.
Philolaos, the Pythagorean
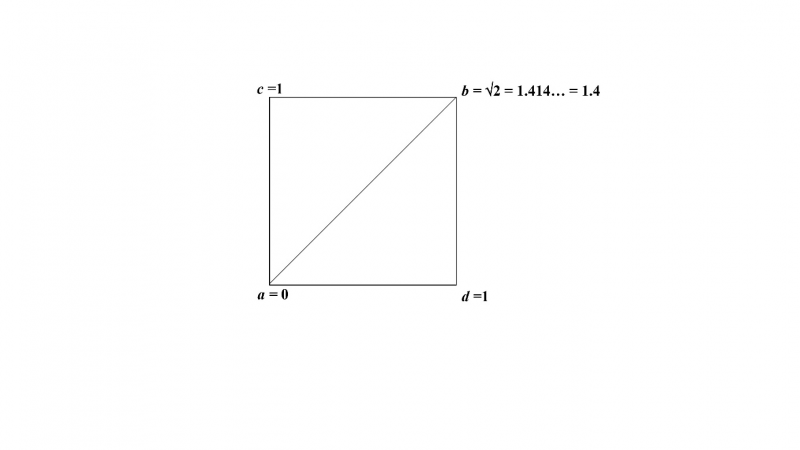
Consider the Pythagorean unit square acbd whose sides are equal to one unit length, as the two-dimensional representation (model) of our universe. We will demonstrate that the square’s diagonal ab is the geometric topos of anything existing as a complex whole or universe possessing the geometric properties of i) complexity, ii) proportionality between its parts, iii) indeterminacy, iv) neutrality (impartiality) v) balance, vi) freedom, vii) free, constant motion at a constant or accelerating speed, and viii) problem-solving action such as resolving conflicts.
There are two complementary ways for the body m to move from a to b. The first is the direct way, along with the diagonal distance ab involving a single displacement; the second is, the indirect way, along with the horizontal distance ad,and the vertical distance db involving two displacements (figure 1.1). The equivalence between these coexisting ways of movement from a to b is expressed by the following synthetic formula:
1.1. ab = ad + db,
which holds that motion along the diagonal ab is equivalent to motion along the horizontal distance ad and the vertical distance db. Because two unequal distances ab and the sum ad + db are equal despite their inequality, we may recast the above synthetic formula in this manner:
1.2. (ab < ad + db)(ab = ad + db).
Formula 1.2 holds that the diagonal distance ab is both unequal and equal to the sum ad + db without contradiction or paradox. In fact, in Euclidean metric geometry, the diagonal ab is less than the sum ad + db, whereas in non-Euclidean, non-metric geometry, ab is equal to the sum ad + db.
Based on the foregoing considerations, we conclude that the diagonal ab is a complex whole or universe receiving simultaneously equal and opposite determinations (parts): for example, the horizontal and vertical parts ad and db, which form a sum to which the complex diagonal ab is both unequal and equal. Moreover, anything existing on the complex diagonal ab,such as the moving body m, is a complex whole or universe traveling simultaneously two different paths, the diagonal path ab and the sum of horizontal and vertical paths ad + db without contradiction or paradox.3
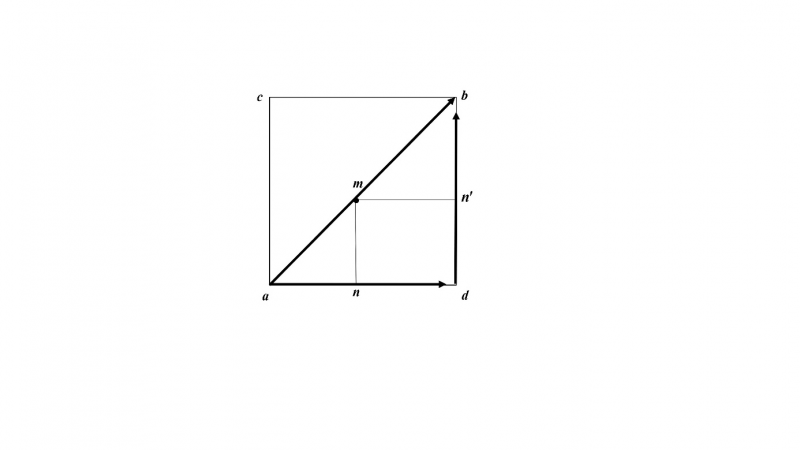
Because the parts ad, db of the complex whole ab form both a sum of separated parts and a totality of conjoined and unified parts as a consequence of the sum’s equality and simultaneity with the single diagonal ab, we may define the diagonal complex whole ab as the sum total of all its parts ad and db:
1. 3. ab = (ad + db)(ad × db),
where + is the sign of addition and × is the sign of conjunction.
If we count each part as 1, then replacing the parts by 1 in the above formula, we obtain the following:
1.4. ab = (1+1)(1×1) = (2 = 1).
This formula states that the complex ab is both many things and one thing ⎯ the sum of at least two things ad and db, which conjoined form one thing, namely the whole ab. Thereby, the diagonal ab verifies the one − many synthetic equivalence principle, which governs the complex whole or universe. The word universe derives from the Latin, uni (“one”) and versus (past participle of the verb vetere, “to turn” or the inverse). The universe is, then, complex and all-embracing, simultaneously one and the inverse, or many without contradiction or paradox. However, if we consider the universe improperly (falsely), that is, as a simple individual, then its opposite determinations are necessarily contradictories (opposites which cannot exist simultaneously) and not contraries (opposites which exist simultaneously) and the idea of the all-embracing universe becomes self-contradictory or paradoxical (see also note 3).
We can also show the equivalence between the diagonal ab and the sum of its parts ad + db by using the one-to-one correspondence method of set theory. If every point m of the diagonal ab corresponds to a unique point n on the horizontal part ad and at the same time to a unique point n′on the vertical part db, then the diagonal ab has the same number of points with the sum of its parts ad + db. Because they have the same number of points, we conclude that ab and ad + db are equal (see formula 1.1).
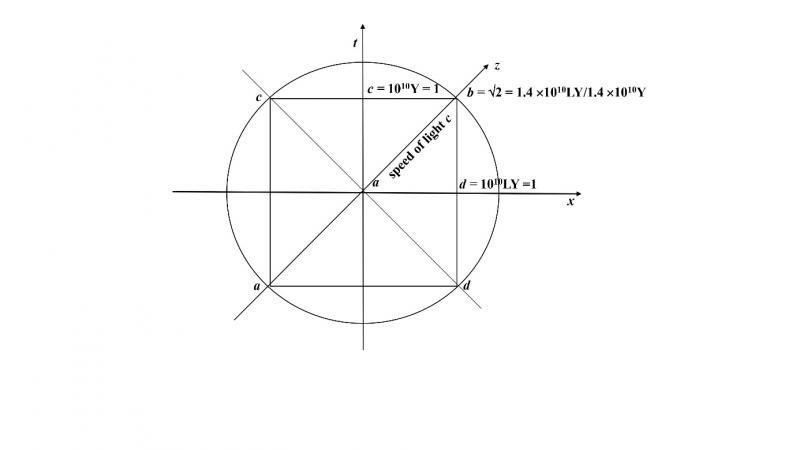
Another way to show the comprehensive and complex nature of the diagonal ab is this way: Let the square’s horizontal side ad represent one unit of space on the space axis x and the square’s vertical side ac represent one unit of time on the time axis t — the diagonal ab on the axis z represents then, the equality of the opposite parts, namely of space and time, which defines the complex two-dimensional universe or whole (figure 1.2). Thus, when a body m travels at a constant speed, or at a constant acceleration, one unit of space ad on the horizontal space axis x at one unit of time ac on the vertical time axis t, it necessarily travels on the square’s diagonal ab, which is the equality of space and time.
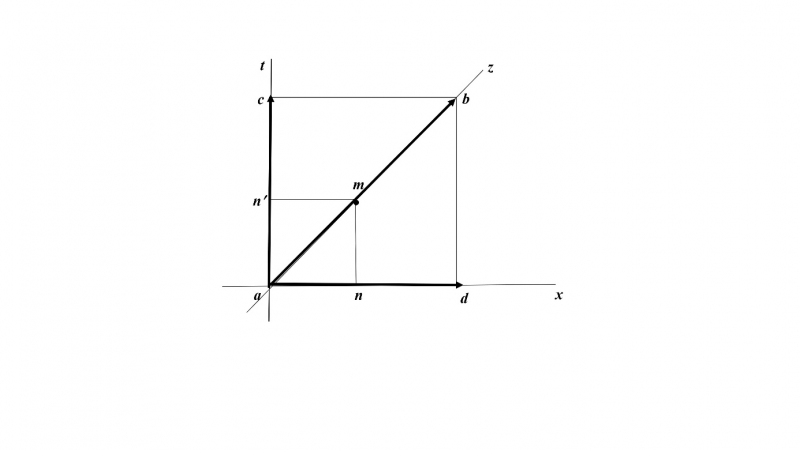
Because the body m travels simultaneously equal units of space ad and time ac, we conclude that their ratio is constant and equal to 1 and that they are equivalent or directly proportional:
1.5. ab =ad/ac = 1 ↔ ad = ac.
Grounded in the formula 1.5, we assert that the square’s diagonal ab is the geometric topos of opposite quantities ad and ac, which are equivalent or directly proportional and have a constant ratio equal to 1. Thus, if one quantity, say ad, is doubled, the other quantity, say ac,is also doubled. Synthetic Logos is the term we use for the unifying link between opposite determinations (parts) ad and ac that obliges them to vary proportionally so that their ratio remains constant. In this way, variation symmetrized by synthetic logos does not disrupt the permanence of the complex two-dimensional universe (space-time) whose geometric topos is the square’s diagonal ab.
The synthetic logos of the square’s diagonal ab
Synthetic logos as a general principle becomes in its modern version the synthetic equivalence principle, which states the equality and simultaneity of opposites; it was formulated by the Greek Ionian philosopher Heraclitus (sixth to fifth century BCE) — the farther of synthetic or dialectic thought. Relative to the formula 1.5, the general synthetic equivalence principle becomes the specific space-time equivalence principle, which stipulates the equivalence and simultaneity of opposites, of the horizontal space distance ad and the vertical time distance ac.
Accordingly, based on the formula 1.5, we state that anything existingin the universe is in its ultimate reality a complex whole m lying on the diagonal ab of the square acbd and therefore lying both on the horizontal space distance ad, more specifically on the point n of ad, and on its equal opposite vertical time distance ac, more specifically on the moment n′ of ac. The complex whole m occupies simultaneously both positions n and n′ in the respective space and time distances ad and ac. A one-dimensional representation of the complex whole is the complex line, which because of its extension occupies both positions n and n′ without contradiction or paradox.
On the other hand, synthetic logos as a mental faculty becomes in its modern version the faculty of synthetic reason, which is the power of our infinite mind (the Greek infinite nous) to conceive the object in its complete and maximum reality (ens realissimum), namely as a real complex whole or universe defined as the sum total of all its determinations (parts) and governed by synthetic logos. The three actions of synthetic logos are thesis, represented by the horizontal part ad; antithesis, represented by the vertical part ac; and synthesis, represented by the square’s diagonal ab comprehending, reconciling and equalizing the orthogonal opposites ad and ac (figure 1.3).
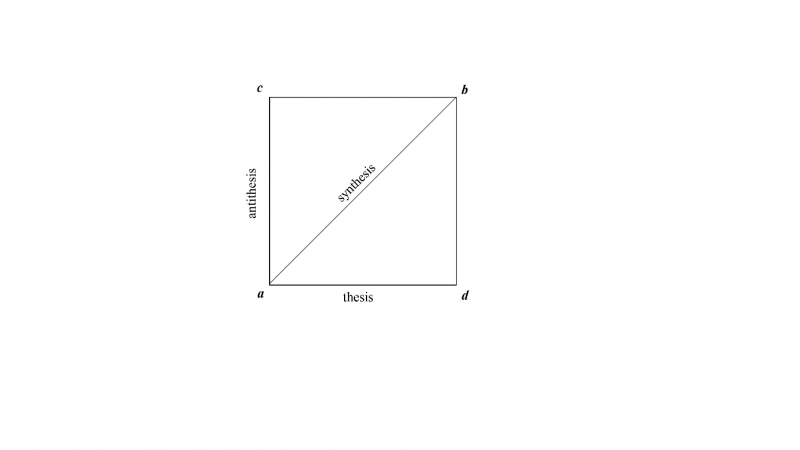
2. The indeterminate logos of the square’s diagonal ab
Another fundamental property of the square’s diagonal ab is its logical and metrical indeterminacy. Because the diagonal ab is equidistant from its opposite sides, it is a third intermediate alternative negating (transcending) both opposite sides (parts- determinations) and in this sense is free from any particular determination. The diagonal ab verifies, therefore, the synthetic principle of the included third, which is a principle of the absolute indetermination of the diagonal ab and which we formalize as follows:
2.1. ab = (ad + ac)′ = (ad)′(ac)′,
where the sign of addition (+) designates either/or and the sign of negation (′) designates not.
Based on formula 2.1, we state that anything existing is an indeterminate whole lying on the diagonal ab and therefore lying neither (not-either) on the horizontal space distance ad (thesis) nor on the vertical time distance ac (anthithesis). The indeterminate whole is neutral and impartial as it lies beyond the partial determinations, i.e. space and time but at the same time synthetic as it embraces them all.
The principle of the included third is the negation of the analytic principle of the excluded third — the principle of the absolute determination of everything — according to which anything existing in the universe is a simple individual, lacking parts or having unequal parts, for example unequal space and time distances. In this case, the simple individual is lying on the diagonal ab of the rectangle acbd whose horizontal side representing the space distance ad and the vertical side representing the time distance ac are unequal. However, such a simple individual exists falsely or incompletely because any being existing in the universe is necessarily in its ultimate reality, a complete whole reflecting the wholeness of the universe. As a complete whole it lies on the diagonal ab of the square acbd whose horizontal side representing the space distance ad and the vertical side representing the vertical time distance ac are equal. Ultimately, we define the diagonal ab as the mutual position (coexistence) and mutual negation (co-absence) of its equal and opposite determinations (parts) ad and ac:
2.2. ab = (ad = ac) = (ad)(ac) = (ad)′(ac)′.
The diagonal space-time distance ab is therefore the geometric topos of any being in the universe, which is in its ultimate nature a complex and indeterminate whole free of all determinations — for example of space and time — by virtue of comprising the totality of determinations.
As a complex whole or universe, the diagonal ab of the unit square acbd verifies the synthetic principle of equivalence, which postulates the equality and coexistence of opposites ad and ac. As an indeterminate whole or universe, the diagonal ab verifies the principle of the included third — the principle of the absolute indetermination of everything — which postulates the equality and co-absence of opposites ad and ac. Insofar as the indeterminate whole ab is equidistant from the opposites ad and ac, it is a balanced being, whereas insofar as it transcends their analytic (contradictory) opposition to find a solution outside and beyond their perennial conflict, it is a problem-free being, in free and constant motion at a constant or accelerated speed.
The circle C is equivalent to the diagonal ab of the Pythagorean square
Before we move on to part 3 of this work, we will demonstrate that the unit circle C, circumscribing the unit square acbd is equivalent to the diagonal ab, which is at the same time the diameter d = 2r (figure 2.1). In other words, we will show that the circle C, which is π times greater than its diameter ab = 2r is equivalent to the diameter ab = 2r. To demonstrate the equivalence between C and ab, we will use the one-to one-correspondence method of set theory. Accordingly, if every point m on ab corresponds to a unique point n on the semicircle C/2= adb and at the same to a unique point n′on the semicircle C/2= acb, then the diagonal ab has the same number of points with the sum of semi-circles C/2 + C/2 defining the unit circle C:
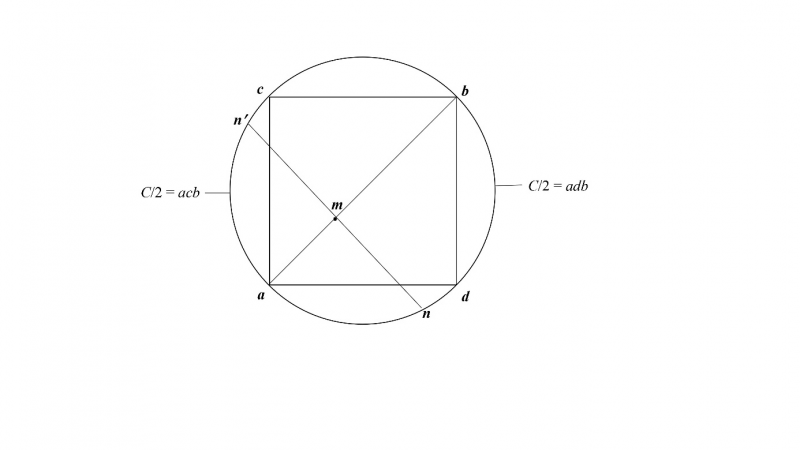
Because the diagonal ab and the unit circle C have the same number of points, we conclude that they are equivalent regardless of their Euclidean metrical inequality:
2.3. ab = C and C = ab,
and that they have due to their equivalence the same intrinsically complex and indeterminate nature. Moreover, as equivalent complex wholes, they constitute the geometric topoi of anything exiting as a complex whole or universe, verifying synthetic principles of existence such as the synthetic equivalence principle, which stipulates the equality and coexistence of opposites, and the synthetic principle of the included third, which stipulates the equality and co-absence (neither/nor) of opposites.
3. The metrical indetermination of the square’s diagonal ab
Let us now examine the metrical indetermination of the diagonal ab of the unit square acbd representing two-dimensionally the universe. Having assumed that each side of the square is equal to one unit length, we measure its diagonal ab by means of the Pythagorean theorem, which we found to be the real finite-infinite number ab = √(ad)2+(db)2 = √12 + 12 = √2 = 1.414….Rounding (finitizing) the real number’s infinite decimal expansion to two significant digits, we write 1.414…= 1.4.
If we consider √2 as a simple point lacking extension, then it necessarily lies somewhere between the points 1.4 and 1.5 on the number line. However, because of its infinite decimal expansion, we do not know where it is exactly located in the interval (1.4, 1.5).4 If we consider the number √2 as a complex line, then it has a continuous extension, which means that it lies everywhere, both on the point 1.4 and on the point 1.5 of its line segment or interval (1.4, 1.5) by passing at once through the intermediate infinity of points; therefore the real number √2 can be equal to any point from 1.4 to 1.5. It follows that the diagonal radius ab = √2 has an indeterminate magnitude, that is, any magnitude ranging from 1.4 to 1.5. In other words the magnitude of the diagonal ab is the line segment or interval (a,b), where a = 1.4 and b = 1.5.
From the computational perspective of analytic reason, the impossibility of determining a unique magnitude to the diagonal ab is interpreted negatively as a sign of our absolute ignorance of its measure. We call negative indeterminacy this absolute ignorance of the real and true magnitude of the diagonal ab, assumed to be simple and one — namely, a simple individual. As we have argued, this negative indeterminacy is the consequence of the impossibility of determining the unique position and value of the number √2 in the line segment or interval (a, b) = (1.4, 1.5).
However, from the non-computational perspective of synthetic reason, the impossibility of determining a unique magnitude to the diagonal ab is interpreted positively — namely as a sign of our complete knowledge of its measure. We call positive indeterminacy this absolute knowledge of the real and true measure of the diagonal ab assumed to be a complex whole having at least two equally real and true magnitudes 1.4 and 1.5 and thus an infinite totality of equally real and true magnitudes occurring within the interval (a, b) = (1.4, 1.5). This positive indeterminacy reflects the real nature of the diagonal ab, conceived as a complex indeterminate whole and at the same time as the geometric topos of anything existing in the universe as a complex indeterminate whole. If anything lies on the diagonal ab of the unit square acbd, then it is necessarily a complex indeterminate whole possessing synthetic and indeterminate logos and conversely, if anything possesses synthetic and indeterminate logos, it necessarily lies on the diagonal ab of the unit square acbd representing our universe (space-time) two-dimensionally.
4. Geometric solution to the mystery of the cosmic expansion rate
Having revealed the intrinsic properties of the square’s diagonal ab, we subsequently proceed to use this diagonal structure of the universe, endowed with synthetic and indeterminate logos, to solve geometrically the mystery of its expansion rate presenting two different values at the same time. To refresh the reader’s memory, the universe’s current expansion rate is called the current Hubble constant H = v/d, which the cosmologists use to connect the universe’s current expansion speed v with its distance from us d.5 It implies, thus, the Hubble law
4.1. v = Hd, where H = v/d,
stating that the recession speed v of a galaxy is proportional to the distance from us d. The farther away the galaxy is from us, the faster it appears to be moving away. If we inverse the Hubble constant H, we obtain the current age t of the Hubble universe:
4.2. 1/H = d/v = t.
The Hubble constant is therefore a cosmological parameter that sets the scale — the age and size — of the universe. Now having defined the Hubble constant, we examine the epistemological question of different measurements assigning different values to it.
Let the unit square acbd circumscribed by a circle of center a and radius ab represent the Hubble universe two-dimensionally. If the square’s horizontal side ad measures the size of the Hubble universe, which is of the order of 1010 = 10 × 109 LY (10 billion light-years) taken as one unit of space, the vertical side ac measures the time (age) of the Hubble universe, which is of the order of 1010=10 × 109 Y(10 billion years) taken as one unit of time, then necessarily the space-time radius of the Hubble universe, which is the square’s diagonal ab, by means of the Pythagorean theorem is ab = √(ad)2+(ac)2 = √12 + 12 = √2 = 1.414…= 1.4 . This measure applied to cosmological dimensions gives relative to space ad the value 1.4 × 1010 = 14 × 109LY (14 billion light-years) and relative to time ac the value 1.4 × 1010 = 14 × 109Y (14 billion years). Their space-time ratio ab = ad/ac =1.4 × 1010LY /1.4 × 1010Y defines the constant speed of light c along the diagonal ab, which we take as a constant of proportionality connecting the space distance ad with the time distance ac. (figure 4.1). As a constant of proportionality unifying opposite (orthogonal) parts, we consider c as equal to unity:
4.3. c = ad/ac =1.4 × 1010LY /1.4 × 1010Y = 1.4×1026m/1.4×3×1017s = 3.333…×108m/s, or, rounding (finitizing) to one significant digit, c = 3×108m/s =1.
As we can see, the diagonal space-time radius ab is measured by the number √2, which insofar as we conceive it as a continuous and extended line, lies everywhere — both on the point 1.4 and on the point 1.5 — by passing at once through the intermediate infinity of points of its line segment or interval (1.4, 1.5) and hence by being equal to any of them (see part 3). In terms of cosmological dimensions, we conclude in an analogical manner that the Hubble universe, whose space-time radius is the complex and indeterminate diagonal ab,has simultaneously the size and age of 1.4 × 1010LY= Y and the equally true size and age of 1.5 × 1010LY = Y by passing at once through the intermediate infinity of equally true sizes and ages greater than 1.4 × 1010LY = Y and smaller than 1.5 × 1010LY =Y. The current Hubble constant H = v/d , which corresponds to the Hubble universe’s current age of 1.4 × 1010 = 14 × 109Y (14 billion years) is 73.5km/s/Mpc, or, rounded to two significant digits, 74km/s/Mpc (74 km per second per megaparsec ); it is obtained from the astrophysical measurements of the late universe (Adam Riess, 2019).6 If we inverse this Hubble constant, we obtain the current age t of the Hubble universe:
4.4. 1/H = d/v = t,
where d = Mpc (one megaparsec) = 106 × 3.09 × 1016 m = 3.09 × 1022 m and v =73.5km/s = 7.35 × 104m/s, and whose value is:
4.5. t = d/v = 3.09 × 1022/7.35 × 104 = 4.20 × 1017s/ 3 × 107s = 1.4 × 1010= 14 × 109 Y (14 billion years).
Similarly, the current Hubble constant H = v/d, which corresponds to the Hubble universe’s equally true current age of 1.5 × 1010 = 15 × 109Y (15 billion years) is 68.6/s/Mpc, or rounded to two significant digits, 69 km/s/Mpc (69 km per second per megaparsec) and is obtained from CMB (cosmic microwave background) measurements of the early universe (Hart, Luke, and Jens Chluba, 2020).7 If we inverse this Hubble constant, we obtain the current age t of the Hubble universe:
4.6. 1/H = d/v = t,
where d = Mpc (one megaparsec) = 106 × 3.09 × 1016 m = 3.09 × 1022 m and v =68.6 km/s = 6.86 × 104m/s, and whose value is:
4.7. t = d/v = 3.09 × 1022/6.86 × 104 = 4.50 × 1017s/ 3 × 107s = 1.5 × 1010= 15 × 109 Y (15 billion years).
The difference between the values 74 and 69km/s/Mpc and therefore between the values 14 and 15 billion years and light-years reflects the different but equivalent ways of measuring the Hubble constant and the age and size of the universe. The inductive method starts with astrophysical measurements in the late or local (here present) universe at a(tnow) and proceeds backward to the origin of the universe at b(t0). From these astrophysical measurements, we derive a current Hubble constant H = v/d equal to 74km/s/Mpc and a cosmic age and size of 1. 4 × 1010 = 14 × 109Y = LY (14 billion years and light-years). The symmetrical opposite deductive method starts with CMB measurements in the early or global (distant past) universe occurring near the origin b(t0) and proceeds forward to the local (hear present) universe at a(tnow). From these CMB measurements performed by the Planck satellite, we derive a current Hubble constant H = v/d equal to 69km/s/Mpc and a cosmic age and size of 1.5 × 1010 = 15 × 109Y = LY (15 billion years and light-years).We have, thus, the space-time interval ab = (a, b), where a = a(tnow) = 1.4 × 1010 and b = b(t0) = 1.5 × 1010 (figure 4.2).
The difference between the two values 74 and 69km/s/Mpc of the Hubble constant must not be interpreted negatively as an unsolvable conflict caused by the impossibility of determining and knowing, which of the alternatives is its only real and true value. This indeterminacy indicates the intrinsically complex and indeterminate nature of the current Hubble constant replicating the complex and indeterminate nature of the universe, whose geometric topos is the square’s diagonal ab. In this sense, the Hubble constant is not a simple determinate quantity— an extensionless point — having at any given time a unique true value, namely either the value a = a(tnow) = 74 or the value b = b(t0) = 69, as the finite analytic paradigm of science claims, but instead a complex indeterminate quantity— an extended line — having both true values a = a(tnow) =74 and b =b(t0) = 69 and therefore an infinite number of equally true values occurring within the line segment or interval ab = (a, b), where a =74 and b = 69.
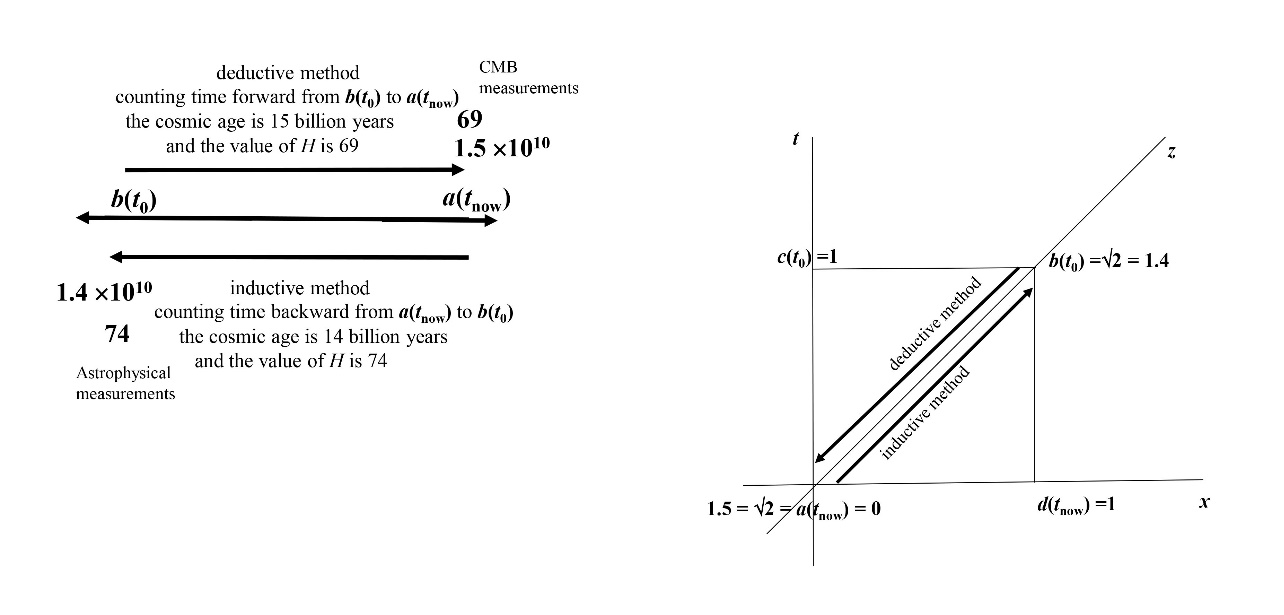
Similarly, we claim that the age and size of the Hubble universe are in their ultimate realities complex indeterminate quantities- –that is, extended complex lines having both true values a = a(tnow) = 1. 4 × 1010 and b = b(t0) =1.5 × 1010 and therefore an infinite number of equally true values occurring within the line segment or interval ab = (a, b), where a = 1.4 × 1010 and b = 1.5 × 1010.
Based on these considerations, we conclude that the infinite number of values of the Hubble constant setting the infinite number of values of the cosmic age and size generates, in turn, an infinite number of equally true models (versions) of the same Hubble universe having the diagonal radius ab = √2 = (1.4, 1.5). These different models of the Hubble universe have different space-time radii — namely, different sizes and ages occurring within the same space-time line segment or interval ab = (a, b) = (1.4 × 1010, 1.5 × 1010) — and different Hubble constants occurring within the same line-like Hubble constant H = ab = (74, 69). Each model describes a particular value of the Hubble constant that determines a particular value of its cosmic age and size, but is constrained by the same Hubble order of magnitude, namely 1010, and by the same speed of light c =1 unifying space with time.
Because our current detectors (neuronal brain and tools) are finite and computational ruled by analytic principles of existence, we arbitrarily select at any given time one and only one true value out the infinite totality of values of the line-like Hubble constant H = ab = (74, 69) which we take as the current or actual Hubble constant. This actual Hubble constant determines, in turn, one and only one true age and true size out of the infinite totality of ages and sizes occurring in the line-like Hubble universe U = ab = (1.4 × 1010, 1.5 × 1010) and thereby one and only one true model of the Hubble universe out of the infinite totality of models, which we take as the actual Hubble universe. Subsequently, grounded in Leibniz’s principle of sufficient reason, we proceed to explain why we have chosen this particular value rather than another of the line-like Hubble constant ab = (74, 69).8 In reality, however, it is immaterial what value we chose to be the current value of the Hubble constant since according to the principle of the equivalence of synthetic logos or reason, all values are equally true and therefore consistent with the universal laws, fundamental principles, and properties of the Hubble universe.
Thus, the Hubble constant is not a simple individual — a point — having at any given time a unique value, say either the value a = 74km/s/Mpc or the value b = 69km/s/Mpc, but a complex whole— a line segment or an interval— having at any given time both true values a = 74 and b = 69 and hence an infinite totality of equally true values occurring within the line-like Hubble constant H = ab = (74, 69). In this sense, Wendy Freedman’s calculation of the Hubble constant assigning to it the value 69.8km/s/Mpc, or rounded to two significant digits, the value 70km/s/Mpc (70kilometers per second per megaparsec) and determining a cosmic age of 1.48 billion years is equally true as it occurs within the line-like Hubble constant roughly midway between the true values a = 74 (Riess team) and b = 69 (Planck team).9 This shows us that ultimately what is significant for rational cosmology is not the measurement of the Hubble constant, which is observer-dependent having any value from 74km/s/Mpc to 69km/s/Mpc but the discovery of an observer-independent unifying link (proportion) between different things — between the expansion speed v of the galactic universe and its distance from us d, which we call synthetic logos.
From the analytic to the synthetic ontology of existence
We use the term positive indeterminacy to mean the indetermination produced by the complete and maximal knowledge of the real object — for example, of the actual Hubble constant — assumed to be a complex indeterminate whole, that is, a line segment or interval ab = (a, b) possessing simultaneously different determinations a = 74 and b = 69 and therefore an infinite totality of determinations occurring within the interval (a, b). Because all determinations of the real object qua complex whole are equally true, we conclude together with the Greek Ionian philosopher Leucippus (fifth century BCE) that nothing is such rather than such — that no Hubble constant has the value 74km/s/Mpc rather than the value 69km/s/Mpc.10 We consider this egalitarian statement as a principle of synthetic logos, which we use to transform the analytic and conflicting opposition between a =74 and b = 69, where either one of the alternatives is true, into a synthetic and complementary opposition where both alternatives are true or false. Through the synthesis of these opposite and equally accurate and true measurements, we obtain the complete and maximum reality of the Hubble constant determining the complete age and size of the Hubble universe from all viewpoints.
At this point, we embrace a fundamental paradigm transformation of the finite analytic paradigm of cosmology into its negation, the infinite synthetic paradigm regarded as the true language of the physical universe, which will help us to correctly and comprehensively interpret the sense-data. The passage from the analytic to the synthetic paradigm proceeds deductively by using the modus ponens and modus tollens rules: If anything that exists — for example, the Hubble constant— is a simple individual, then it has at any given time, taken as the current time, a unique value, which is either a = 74 or b =69. However, measurements taken from maximally different viewpoints a(tnow) and b(t0) of the universe show that the current Hubble constant simultaneously receives both values a = 74 and b = 69. It follows that it is false that the Hubble constant is a simple individual — a simple determinate quantity verifying analytic principles of existence and represented geometrically by the point. If the proposition “the Hubble constant is a simple individual” is false, then its negation “the Hubble constant is a complex whole” must be true. We then conclude that the Hubble constant is a complex whole — a complex indeterminate quantity verifying synthetic principles of existence and represented geometrically by the line.
The analytic paradigm of science has originated in the analytic logic of the Greek philosopher Aristotle (fourth century BCE) equally called organon (tool). Analytic logic reflects the way our finite analytic detectors — our neuronal brain and tools — operate. By observing them, Aristotle postulated the analytic principles that govern their analytic behavior. As Aristotle put it “No senses applied to the object tells us that the same object is simultaneously so and not so”.11 If we project these principles outward they become the principles that govern the physical universe and anything existing in the universe. However, we commit an epistemological error when we consider these projected analytic principles as if they were the real and true principles of the universe in itself, whereas in reality, they are the principles of the universe submitted to our analytic perception.
A fundamental principle of existence is the principle of contradiction, which stipulates that nothing is simultaneously (both) a and a′(not-a) called b:
4.8. (a = b)′ or (ab)′,
where (′) stands for negation, falsity or impossibility, and = stands for equality, unity, and simultaneity. It follows that everything is either a or b, that is, either a is true or b is true:
4.9. a + b = (a =1) + (b = 1)
where + stands for either/or and 1 stands for true.
This formula constitutes the analytic principle of the excluded third and shows the object as an individual made of contradictory, isolated parts a and b, which are discontinuous points. Both analytic principles assume that anything existing in the physical universe is an individual — a simple point — deprived of extension and therefore incapable of containing both determinations a and b within the same point-object. However, if we would like to have the complete and maximal knowledge of the object, that is to say, to see the object from all viewpoints (parts-determinations), and hence attain its ultimate reality and truth, we must then assume that the object is a complex whole or universe — a complex line — having an extension and therefore capable of containing at least two viewpoints a and b and therefore an infinite totality of viewpoints occurring within the line-object ab = (a, b).
We then replace the analytic principle of contradiction, which is a principle of existence as a simple individual, with the synthetic principle of equivalence, which is a principle of existence as a complex whole. According to it, everything is simultaneously a and a′(not-a) called b — that is, both a and b are true relative to the same thing:
4.10. a = b or ab =(a =1) (b =1),
where = stands for equality, unity, and simultaneity and 1 stands for true.
This formula shows the object as a continuous line ab made of equal and coexisting parts a and b, which are continuous lines.
The synthetic paradigm of science has originated in the synthetic logos of the Greek Ionian philosopher Heraclitus (sixth century BCE) who considered it as the principle of unity of opposites occurring beneath or beyond the surface of phenomena of the universe. As a unifying principle, synthetic logos assigns an invisible unity, intelligibility, and balance to the universe. Because our analytic senses distinguish and separate, the unity of the universe is realized by synthetic logos, which is not only a unifying principle but also, as we have already claimed in part 1, a mental faculty of our infinite mind aiming at the complete and maximum knowledge of the universe — of every object — defined as the sum total of its infinite number of determinations (parts). Because we have access to infinity through its finite part to know completely and maximally the universe ⎯ that is, any object within it, it is necessary and sufficient to know through different measurements its finite number of determinations a and b and through these finite determinations to determine and know, by the finite-infinite equivalence principle, its infinite number of determinations occurring within the line-object ab = (a, b). Similarly, to know completely and maximally the line-like Hubble constant H = ab = (a =74, b = 69), it is necessary and sufficient to know through different measurements its finite number of values, namely the two values a = 74 and b =69 —in order to determine and know its infinite totality of values occurring within its line segment or interval ab.
Based on these considerations, we conclude that the Hubble tension between the values a = 74 and b =69 exists because we tacitly assume an analytic ontology of the Hubble constant that generates an unsolvable conflict between them. Relative to a unique observer who starts his measurements either from the local viewpoint a(tnow) and hence from the here and present universe, or the global viewpoint b(t0) and hence from the distant and past universe, the Hubble constant H is a simple individual— a simple quantity having at any given time, considered as the current time, a unique value that verifies analytic principles of existence. The conflict between the alternative viewpoints a(tnow), giving the value 74, and that of b(t0), giving the value 69, remains unsolvable within the analytic paradigm of the unique observer. However, once we introduce the pair of equal and opposite observers, namely the observer a measuring H from the local viewpoint a(tnow) and the observer b measuring H from the global viewpoint b(t0), the analytic (contradictory) opposition between these alternative viewpoints becomes a conflict-free synthetic opposition where they are simultaneous and equally true or false.
The sum total of all observations ranging from a = 74 to b = 69 by passing through the infinite totality of potential observations occurring within the line segment or interval ab =(a, b) defines our complete and maximum measurement and knowledge of the Hubble constant whose ultimate reality is that of being a complex indeterminate whole.
If the finite Hubble universe and any of its correlated finite quantities such as the Hubble constant determining its age and size are in their ultimate realities equivalent to the infinite physical whole or universe, which we defined as the sum total of its infinite number of parts, we then conclude that any finite part of the infinite universe is a replica of the infinite universe and conversely the infinite universe is equal to any of its finite parts. This constitutes the non-Euclidean synthetic principle of self-similarity, which governs the self-contained infinite universe being both a finite part, namely the Hubble universe, and an infinite physical whole in itself. If the infinite physical universe is a continuous line whose finite parts, for example, the Hubble universe, the Hubble constant, and the Hubble age and size are in their ultimate realities complex infinite wholes — that is, continuous lines — then the real continuum of the physical universe is the infinite whole of infinite wholes represented by the line of lines and governed by synthetic principles of existence.
The passage from analytic ontology favoring the analytic paradigm of dogmatic science to synthetic ontology favoring the synthetic paradigm of non-dogmatic science grounded in synthetic logos is analogous to the passage from natural numbers, which are uniquely finite point-numbers verifying analytic principles of existence, to real numbers, which are both finite and infinite line-numbers verifying synthetic principles of existence and constitute the ultimate reality of natural numbers. The real physical universe is not, therefore, a continuum of natural point-numbers — a line of points — in isolation between them, as dogmatic science claims, but instead a continuum of real line-numbers — a line of lines — in immediate contact between them that replicate the infinite physical whole.
To put it all in perspective and solve the Hubble cosmic crisis, what we need is not a “new physics,” that is, the discovery of new phenomena — of new sense-data — but rather the intelligible reinterpretation of the given sense-data in the light of a holistic and synthetic ontology of existence.
© Ion Soteropoulos, Paris, March 15, 2021
Notes
1 Aristotle, Metaphysique A, 5
2 Aristotle, Physique III(4) 203 a10
3 According to Aristotle, anything possessing simultaneously opposite determinations, which he calls contraries, belongs to the class of universals, whereas anything possessing non-simultaneously, that is, successively opposite determinations is an individual (Metaphysique I, 10, 1058b, 30-35). To the Aristotelian definition of the individual, we add that the successive determinations of the individual are necessarily contradictory because of their impossible coexistence.
4 Let us assume the following: If there is the square root of two (√2), then there is a number a such that a × a = 2. Grounded in this assumption let us try to locate √2 on the number line. If we suppose that √2 lies on the point 1.4, then 1.4 × 1.4 = 1.96, which is less than 2. If we suppose that √2 lies on the point 1.5, then 1.5 × 1.5 = 2.25, which is greater than 2. It follows that the number √2 lies neither on 1.4 nor on 1.5 but instead somewhere between them. However, because of the infinite decimal expansion of √2 we do not know at which point it is located between 1.4 and 1.5. This impossibility of determining the location of √2 in the interval (1.4, 1.5) indicates our ignorance of the determinate and true position and value of √2.
5 To express the current value of the Hubble constant the cosmologists assign the subscript 0 to H: H0.
6 To learn about Adam Riess’ s calculations of the Hubble constant, visit: https://www.nasa.gov/feature/goddard/2019/new-hubble-constant-measurement-adds-to-mystery-of-universe-s-expansion-rate. Last updated: July, 2019. Editor Rob Garner.
7 Hart, Luke and Jens Chluba. “Updated fundamental constant constraints from Planck 2018 data and possible relations to the Hubble tension” in ArXiv: 1912. 03986V2 [astro-ph], May 20, 2020.
8 Leibniz’s principle of sufficient reason poses the analytic question Why is something such rather than such? This question aims at explaining the arbitrary choice of one alternative against the other in agreement with the analytic principle of the excluded third. Thus, the sufficient reason principle is a consequence of the finite analytic behavior of our neuronal brain. An object intuited by our infinite mind as a complex whole or universe — that is, as a complex extended line simultaneously receiving contrary (equal opposite) determinations a and b, is perceived by our finite neuronal brain and its tools as if it were a simple individual — that is, as an extensionless point possessing at any given time a unique determination, for example, either determination a or determination b. As a simple individual having at any given time a unique determination, we ask ourselves Leibniz’s analytic question. Now the impossibility of determining which of the alternative determinations is the true determination of the real object defines the state of negative indeterminacy expressing our absolute ignorance of the real object assumed by our finite brain and its faculty of analytic reason to be a simple determinate individual, that is to say an extensionless point (see part 3).
9 For Wendy Freedman’s calculations of the Hubble constant, visit https://www.nasa.gov/feature/goddard/2019/new-hubble-constant-measurement-adds-to-mystery-of-universe-s-expansion-rate. Last updated: July, 2019. Editor Rob Garner.
By inversing the Hubble constant H = v/d = 69.8km/s/Mpc, we derive the corresponding equally true current age of the Hubble universe, which is 1/H = d/v =t = 3.09 × 1022 m /6.98 × 104m/s = 4.426 × 1017s/3 × 107s = 1.48 × 1010 = 14.8 × 109Y (14.8 billion years).
10 The Greek Ionian atomist philosopher Leucippus and his associate Democritus (fifth century BCE) postulated an infinite number of atoms in perpetual motion and held that their shapes and sizes are infinite in number, based on the egalitarian principle that “nothing is such rather than such” (Kirk, Raven and Schofield. The Presocratic Philosophers. Cambridge, UK: Cambridge University Press, 1988, 416). In this way, they linked infinity with the principle of the uniformity and equality of atoms. Accordingly, if there is an infinite number of atoms, then by virtue of the principle of the uniformity and equality between the number of the atoms and the number of their shapes and sizes, there is necessarily an infinite number of shapes and sizes that are equally real and true.
11 Métaphysique. Trad. J.Tricot. Paris: Librairie Philosophique J. Vrin, 1984, Γ4, 10106, 15-20.